-
1
Baake M, Kramer P, Schlottmann M, and Zeidler D,
Planar patterns with fivefold symmetry as sections of periodic structures in 4-space,
In J Mod Phys B 4 (1990) 2217-68
-
2
-
3
-
4
Bravais A,
Les systemes formes par des points distribues regulierement sur un plan ou
dans l' espace,
J Ecole Polytech 19 (1850) 1-128
-
5
de Bruijn N G,
Algebraic theory of Penrose's non-periodic tilings of the plane I,
Proc Koninklijke Nederlandse Akademie van Wetenschapen, 84 (1981) 39-52
-
6
de Bruijn N G,
Algebraic theory of Penrose's non-periodic tilings of the plane II,
Proc Koninklijke Nederlandse Akademie van Wetenschapen 84 (1981) 53-66
-
7
Brown H, Bülow R, Neubüser J,
Wondratschek H and Zassenhaus H,
Crystallographic groups of 4-dimensional space, Wiley, New York 1978
-
8
Conway J H and Sloane N J A,
Sphere packings, lattices and groups,
Springer New York 1988
-
9
-
10
Dürer Albrecht,
Unterweisung der Messung,
Nürnberg 1525, reprint Nördlingen 1983
-
11
-
12
-
13
-
14
-
15
Janner A,
Modulated space groups,
in: Proc 5th Int Coll Group theoretical Methods in Physics,
Montreal 1976, Academic Press, New York
-
16
Kepler J,
Gesammelte Werke KGW 1-24,
Ed. Max Caspar,
München starting 1937
-
17
Kepler J,
Strena seu de nive sexangula
in:
[16] KGW IV (1941): KLeinere Schriften 1602-1611
-
18
Kepler J,
Mysterium Cosmographicum
in;
[16] KGW I (1937)
-
19
Kepler J,
Harmonices Mundi Libri V
in:
[16] KGW VI (1940)
-
20
-
21
-
22
Kramer P and Kramer L,
Diffraction and layer structure of a quasilattice
Z. Naturforsch. 40 a (1985) 1162-1163
-
23
Kramer P,
Nichtperiodische Quasikristalle mit fünfzähliger Symmetrie,
Phys. Blätter 41 (1985) 103-4
-
24
Kramer P,
Grundgedanken zur Symmetrie im Werk von Johannes Kepler,
in:
[48] (1986) Band 1, p. 115-27
-
25
Kramer P and Kramer L,
Icosahedral tiling model projected from the 6-dimensional hypercubic lattice, photograph, in:
[48] (1986) Band 3, p. 91
-
26
-
27
-
28
-
29
-
30
-
31
Kramer P, Quandt A, Schlottmann M, and Schneider T,
Atomic clusters and electrons in the Burkov model of 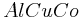
,
Phys Rev B 51 (1995) 8815
-
32
Kramer P, Quandt A, Schneider T and Teuscher H,
Simulation of Mössbauer absorption spectra for decagonal 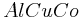
,
Phys Rev B 55 (1997)
-
33
-
34
Kramer P, Papadopolos Z, Eds.
Coverings of Discrete Quasiperiodic Sets,
Springer, Berlin 2003
-
35
Kramer P,
Quasiperiodic systems,
in: Encyclopedia of Mathematical Physics, Eds. J-P Francoise,
G L Naber, Sh Tsun Tsou,
Elsevier, Amsterdam (2006) pp. 308-315
-
36
-
37
-
38
-
39
-
40
-
41
Kramer P,
Platonic topology and CMB fluctuations: Homotopy, anisotropy, and multipole selection rules.
arXiv:0909.2758
-
42
Lax M,
Symmetry principles in solid state and molecular physics.
Wiley, New York (1974)
-
43
-
44
-
45
-
46
-
47
Mackay A L,
Crystallography and the Penrose Pattern,
Physica 114 A (1982) 609-13
-
48
Mazzola G Ed.,
Symmetrie in Kunst, Natur und Wissenschaft,
Katalog der Ausstellung Mathildenhöhe Darmstadt 1. Juni bis 24. August 1986,
Band 1 Texte, Band 2 Kunst, Band 3 Spiel, Natur und Wissenschaft
Verlag E Roether, Darmstadt 1986
-
49
Mosseri R and Sadoc J F,
Two and three dimensional non-periodic networks obtained from self-similar tiling,
in: The structure of non-crystalline materials,
Taylor and Francis, London 1982, pp. 137-50
-
50
Nelson D R,
Quasicrystals, Scientific American 255 (1985) 42-51
-
51
Penrose R,
The role of Aesthetics in Pure and Applied Mathematical Research,
Bull Inst Math and its Appl 10 (1974) 266-71
-
52
Platon,
Timaios,
in: Sämtliche Werke VIII,
Insel Verlag, Frankfurt 1991, pp. 197-425
-
53
-
54
Seifert H and Threlfall W,
Lehrbuch der Topologie.
Leipzig 1934, Chelsea Reprint, New York 1980
-
55
Shechtman D, Blech I, Gratias D, and Cahn J W,
Metallic phase with long-range orientational order and no translational symmetry,
Phys Rev Lett 53 (1984) 1951-3
-
56
Schwarzenberger R L E,
N-dimensional Crystallography,
Pitman, San Francisco 1980
-
57
Wigner E P,
Group theory and its application to the quantum mechanics of
atomic spectra,
Academic Press, New York 1959
-
58
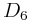 and icosahedral quasicrystals,
in: Frank A, Seligman T H and Wolf B, (eds.),
Group theory in Physics,
American Institute of Physics Conf Proc 266, New York 1992, 179-200
and icosahedral quasicrystals,
in: Frank A, Seligman T H and Wolf B, (eds.),
Group theory in Physics,
American Institute of Physics Conf Proc 266, New York 1992, 179-200
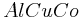 ,
Phys Rev B 51 (1995) 8815
,
Phys Rev B 51 (1995) 8815
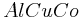 ,
Phys Rev B 55 (1997)
,
Phys Rev B 55 (1997)
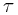 -inflation to
-inflation to 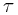 -wavelets,
-wavelets,