Periods in time governs the composition of days, months and years. Periodic repetitions, with identical atomic arrays as building blocks, constitute the structure of crystals. The periodic repetition pattern is described by a lattice. Quasicrystals exemplify repetition patterns from atomic arrays which are aperiodic or quasiperiodic and lack a lattice.
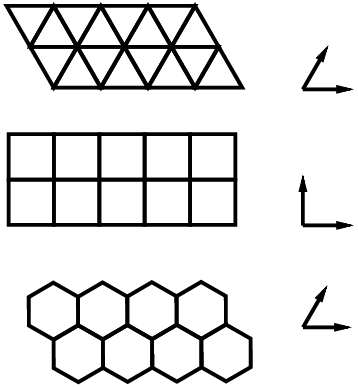
There are tilings of the plane by regular polygons. The plane together with the standard Euclidean distance law is an Euclidean space, and we denote this Euclidean plane as E2. For regular triangles, squares and hexagons, there are repetition patterns which tile the plane periodically, see Fig. 1. Suppose we translate a copy of a tiling in Fig. 1, extended over the full plane, along a translation vector such that after the translation any translated polygon coincides with an unshifted one. Such a translation is a geometric period of the tiling. Pairs of shortest translation vectors are shown in Fig. 1. Any integer linear combination of these pairs yields another translation vector. The set of all these linear combinations forms a lattice in the plane, and each pair of vectors forms a lattice basis.

Fig. 1. Periodic tilings and lattices. Left: Patches from three (infinite) periodic tilings of the plane by triangles, squares, and hexagons. Right: Pairs of shortest translation vectors corresponding to each of the three tilings. It will be shown later, see Fig. 5, that the triangular and the hexagonal tiling are related by duality.
It turns out that there is no tiling of the plane by regular pentagons. To put regular pentagons into a tiling, one must avoid gaps by use of at least a second tile of different shape. Moreover the resulting tiling is not necessarily periodic.
Example 2.1: Albrecht Dürer in his book Unterweisung der Messung (1525) [10] drew a tiling of the plane from two tiles of pentagonal and rhombus shape, Fig. 2.
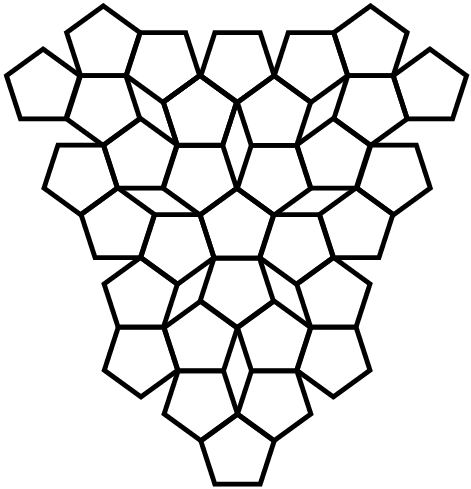
Fig. 2. Aperiodic tiling 1. An aperiodic tiling of the plane by pentagons and rhombs adapted from Albrecht Dürer (1525), Unterweisung der Messung, [10].
Example 2.2: Johannes Kepler made significant contributions to the discovery of symmetry in nature, compare [22]. In his Mysterium Cosmographicum (1596) [17] Kepler studied the five regular polytopes to find the distance law of planets from the sun. He supplemented the list of regular polytopes by two new non-convex star-polytopes. In [16], Strena seu de nive sexangula (1611), and in [18], Harmonices Mundi (1619), he moved on from tilings of the 2-sphere to tilings of the plane by polygons and of space by polytopes. He noted as Dürer that an attempt at tiling with pentagons would leave gaps. When one looks at the location of the tiles in Kepler’s tilings of the plane, compare [22], one again observes two distinct types: In tilings with one type of triangular, square, and hexagonal tiles, Fig. 1, the repetition pattern of the tiles is periodic. In Dürers tiling with pentagons and rhombs Fig. 2, and in Keplers tiling with pentagons, decagons and five-stars Fig. 3, the repetition pattern does not show any periodicity and so is aperiodic. Kepler in [16] also invented the triacontahedron, a polytope of icosahedral point symmetry bounded by thirty rhombus faces. This polytope now plays an important part in the theory of icosahedral quasicrystals, see section 7 and Fig. 11.
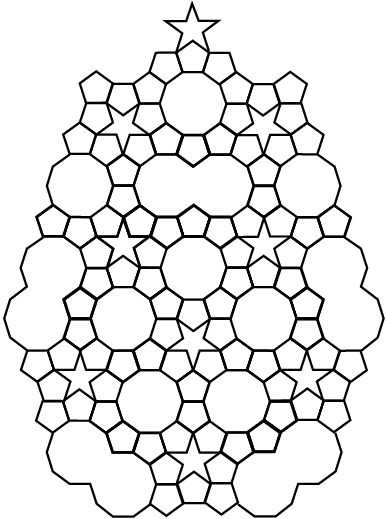
Fig. 3. Aperiodic tiling 2. An aperiodic tiling of the plane by pentagons, (overlapping) decagons, and five-stars adapted from Johannes Kepler (1619), Harmonices Mundi, [18].
In physical space of three dimensions, which we denote as E3, regular planar surfaces had of course been observed long ago as boundaries of crystals. Bravais [4] in 1850 provided a mathematical explanation of the angular relations between adjacent planar faces. He postulated that underlying a crystal there is a three-dimensional crystal lattice Λ, that is a set of points repeated periodically in three independent directions of E3. Given a similar but planar periodic sublattice, a 3-dimensional lattice can be built by periodically repeating this sublattice in a direction out of its plane. Such a sublattice is called a netplane of the crystal. Bravais postulated that the surfaces of a crystal are formed by netplanes of the highest point density. This purely geometric prediction could be macroscopically confirmed, a long time before the atomic structure of lattices could be analyzed.
The lattice idea can be reformulated in terms of translational symmetry: Consider a rigid translation which shifts any initial point of a lattice into another lattice point. The collection of all these translations forms the translation group of the lattice. Related to the notion of a lattice is the notion of a crystal unit cell, a polytope such that its translates tile the crystal periodically without gaps or overlaps.
A point group, with center at a lattice point, whose operations rotate the lattice into itself, is called crystallographic. The cyclic point group C5 of the regular pentagon is not compatible with any 2D lattice, and the iscosahedral point group is not compatible with any 3-dimensional lattice. These groups are therefore called non-crystallographic. This notion depends on the dimension of the space under consideration, so that point groups non-crystallographic in 3 dimensions can become crystallographic in a lattice of n-dimensional space for n > 3.
The repetition pattern of pentagons in Dürers and in Kepler’s examples requires the step from periodicity to aperiodicity or quasi-periodicity.