1.3 Periodic crystals and point spectra in diffraction.

A geometric pattern can be characterized by studying how it can be mapped into itself. For periodic patterns these mappings are translations. The set of these translations is the lattice. If the pattern can be described by a function defined on a geometric background, the Fourier series allows to break this function additively into elementary periodic functions like Sinus and Cosine.

A lattice Λ is carried into itself by its translational symmetry group of discrete translations. Since the geometric correspondence between lattice points and translational symmetry operations is one-to-one, we may denote the translational symmetry group by the symbol Λ for the lattice. So far the translation or point group was acting geometrically as a mapping of points into image points of space. Given a real function f(x) defined on all points say of the plane, its functional values can be viewed as a landscape over this plane. We can define an action of a translation or rotation group element g on this function by a map from f(x) to a new function (T_gf)(x) such that the landscape of all functional values of f(x) is translated or rotated according to the chosen group element g. The symbol T_g is the name of this new operation of g G on a function. The formal prescription for this mapping of functions is

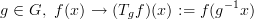(1)

Use of the inverse g^-1 in this definition is necessary if we want successive operations on a function to follow the group multiplication rule,

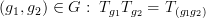(2)

i. e. to give a homomorphism, see [47] pp. 102-11.

The systematic classification of lattices in Eⁿ is the task of n-dimensional crystallography, which in [7] and in [46] is developed from mathematical work by Hermann [13] and Zassenhaus [48].

If eq. 1 is applied to functions on E¹, we can in particular characterize functions f^p(x) periodic under Λ by the property

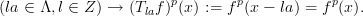(3)

Any periodic real- or complex-valued functions on the real line E¹ with primitive period a, takes values on E¹ which are completely determined by those on the interval 0 ≤ x < a. This interval is called the fundamental domain of the periodic function. The notion of a fundamental domain extends to lattices in the space Eⁿ.

Periodicity in coordinate space has significant consequences for the Fourier analysis. Any periodic function on the line can be developed into a Fourier series

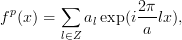(4)

with Fourier coefficients given by the integrals

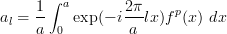(5)

over the fundamental domain. If the exponentials in eq. 4 are decomposed into sines and cosines, the complex Fourier series becomes a series in these elementary trigonometric functions. The points x = la,l Z form the lattice Λ for the periodic function f^p(x). In crystallography it is customary to define on a real line called k-space the reciprocal lattice Λ^R with points k^R Λ^R : k^R = 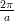l, l Z. Then the Fourier coefficients eq. 5 can be assigned in k-space to the points of the reciprocal lattice.
Similarly, n-fold periodic functions on Eⁿ may be developed into an n-fold Fourier series which then is interpreted as a function on a reciprocal lattice Λ^R on a k-space of dimension n.

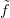For a general function f(x), x Eⁿ with reasonable properties there exists a Fourier integral transform (k), which is a new function on k-space. The fact that for periodic functions this Fourier integral transform reduces to the Fourier series eq. 4, with coefficients attached to the discrete subset of points on the reciprocal lattice Λ^R, is expressed by saying that the Fourier spectrum is pure point.

These relations have observable consequences for the diffraction of waves by periodic distributions of matter: In the so-called Born approximation, the angular distribution of the scattered waves displays sharp diffraction peaks which are labelled by the points from the reciprocal lattice. The diffraction pattern can also be geometrically described in terms of Laue-Bragg reflections from the netplanes of the lattice. Crystallography as developed in the 19th and 20th century employs throughout this fundamental relation between periodic structures and diffraction. It offers experimental access to the periodic atomic structure postulated by Bravais.