1.4 Aperiodic tilings from scaling.
Increasing the length scale of a geometric pattern uniformly in all directions is
termed a scaling. If the image points of a scaled pattern fall on a set of preimages,
we speak of a scaling symmetry or a self-similarity. These play an importants part
in quasicrystals.
At the Institute of Theoretical Physics of the Eberhard-Karls-Universität
Tübingen, I established in 1964 a research group on Symmetry in Physics.
Penrose [42] in 1974 had devised a planar rhombus tiling from scaling
properties. In 1980 I became interested in non-periodic tilings of E3 with
non-crystallographic point symmetry, built from a finite family of tiles. The
hope was that these tiles would generalize the atomic cells of crystals into building
blocks for aperiodic tilings.
The result was the publication [19] in 1982. I started from a dodecahedron of
icosahedral symmetry and formed its central star extension. I devised seven tiles
as building blocks of the dodecahedron. These tiles had the property of
self-similarity: Copies of any one of them, scaled by a power of the golden section
number τ := 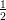 (1 +
(1 + 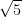 ), could be packed from the original tiles. It followed that,
by use of copies from the fixed set of seven tiles, one can build up a dodecahedral
space filling of 3-space with central icosahedral symmetry of any size. The
abstract of this publication reads:
), could be packed from the original tiles. It followed that,
by use of copies from the fixed set of seven tiles, one can build up a dodecahedral
space filling of 3-space with central icosahedral symmetry of any size. The
abstract of this publication reads:
It is shown that copies of seven cells suffice to fill any region of Euclidean
three-dimensional space. The seven elementary cells have four basic polyhedral
shapesand three of them appear in two different sizes. The space filling
is non-periodic, has a central point, and preserves the full icosahedral
group.
The composition rules are illustated in 12 Figures of [19]. This set of seven tiles
was revised in 1982 by Mosseri and Sadoc [40], who reduced the set from seven to
four tiles and with them constructed a new tiling by scaling. A scaling
construction for an aperiodic tiling has the virtue that no additional dimension is
required. On the other hand, scaling offers no obvious access to the Fourier
properties of the pattern generated. For the Penrose tiling Mackay [37], [38]
conjectured that its Fourier transform may have a point spectrum. That this
conjecture is correct follows by its projection from a lattice, see section 7. It
appears from work by Radin [44] that certain patterns generated by scaling do not
have simple Fourier properties. D Levine and P J Steinhardt, in [34] (received
on Nov 2, 1984), published in 1984 after the experimental discovery of
quasicrystals, used self-similarity to construct an icosahedral quasiperiodic
structure.
Lattices in En may have scaling symmetries which under projection, section 5,
yield scaling symmetries of the tiling. A particularly simple scaling symmetry of a
tiling is stone-inflation; Here the scaled tiles can be decomposed into their
unscaled preimages. In all cases of lattice scaling the quasiperiodic Fourier
properties are maintained. Scaling symmetry will be discussed for the lattice Z2
and the Fibonacci tiling after Fig. 6, and for the planar Penrose tiling projected
from A4 in Fig. 9. For the lattice D6 the scaling is analyzed by lattice theory in
[32] pp. 137-40.
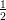 (1 +
(1 + 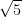 ), could be packed from the original tiles. It followed that,
by use of copies from the fixed set of seven tiles, one can build up a dodecahedral
space filling of 3-space with central icosahedral symmetry of any size. The
abstract of this publication reads:
), could be packed from the original tiles. It followed that,
by use of copies from the fixed set of seven tiles, one can build up a dodecahedral
space filling of 3-space with central icosahedral symmetry of any size. The
abstract of this publication reads: