§ 2.1. Basic concepts.

Topology of manifolds explores properties invariant under continuous deformations. In homotopy theory one examines these properties with the help of closed loops or paths running on the manifold.

In homotopy directed closed loops, returning to a on the manifold to fixed reference point are employed to characterize the topology of a manifold ${\cal M}$ . Loops which can be continuously deformed into one another are identified. The inverse loop is defined by inverting the direction along a given loop. Any two loops are composed by concatenation. Loop concatenation together with inversion generate the first homotopy group $\pi _{1}({\cal M})$ of a manifold, also called its fundamenta group.

Example 1a: Consider the circle ${\cal M}=S^{1}$ . Upon choosing a fixed point, any closed loop can surround it $n$ times clockwise or anti-clockwise. For fixed $n$ , these two loops are inverse to one another. Concatenation generates the infinite cyclic group $C_{{\infty}}$ , so we have $\pi _{1}(S^{1})=C_{{\infty}}$ .

Figure 12. Circle: The unit interval $J=\left[-\frac{1}{2},\frac{1}{2}\right]$ is the image of the circle $S^{1}$ on the real line $R^{1}$ . The real line is tiled by copies of this interval.

An important notion in the topology of manifolds is the universal covering space. For given ${\cal M}$ this is a simply connected manifold $\tilde{\cal M}$ which admits a map ${\cal M}\rightarrow\tilde{{\cal M}}$ such that $\tilde{\cal M}$ is tiled by copies of ${\cal M}$ . On a simply connected manifold, any loop can be contracted to the identity, and the homotopy group is trivial.

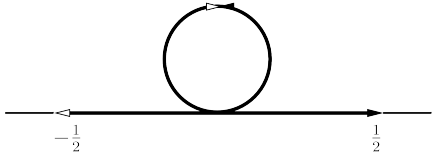
Example 1b: The circle $S^{1}$ can be mapped to the interval $x:-1/2<x\leq 1/2$ on the real line $R^{1}$ , Fig.12 . Its topological closure requires to identify the end points of the interval. Thus the real line is the universal cover of the circle. The images of the interval $J$ under discrete translations by $\pm n$ for $n$ integer form a tiling of the real line $R^{1}$ .