§ 2.5. Spherical 3-manifolds.
Spherical 3-manifolds have the 3-sphere ![]() as their simply connected universal cover.
as their simply connected universal cover.
In line with the reasoning given above, any spherical 3-manifold forms the prototile
of a tiling of the 3-sphere. A particular family of prototiles arises from the
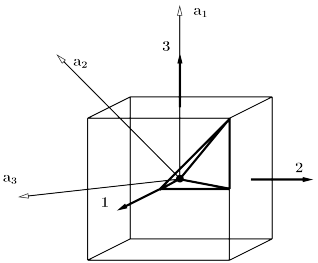
five regular Platonic polyhedra: the tetrahedron, cube, octahedron, dodecahedron and icosahedron in their spherical form. These polyhedra are bounded by reflection hyperplanes passing through the origin of the 3-sphere embedded
in the space ![]() . The so-called Weyl reflections are uniquely characterized as
. The so-called Weyl reflections are uniquely characterized as ![]() by a unit vector
by a unit vector
![]() perpendicular to the reflecting hyperplane. Groups generated by Weyl reflections are
Coxeter groups
perpendicular to the reflecting hyperplane. Groups generated by Weyl reflections are
Coxeter groups
![]() denoted by diagrams. In Table 15
we list sets of four Weyl vectors
appropriate for the Coxeter groups, and corresponding Platonic spherical polyhedra given in Table 2.
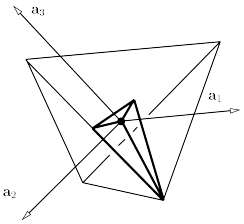
Sets of four Coxeter reflection planes bound what are called Coxeter simplices. The Platonic polyhedra
consist of all simplices sharing a single vertex.
denoted by diagrams. In Table 15
we list sets of four Weyl vectors
appropriate for the Coxeter groups, and corresponding Platonic spherical polyhedra given in Table 2.
Sets of four Coxeter reflection planes bound what are called Coxeter simplices. The Platonic polyhedra
consist of all simplices sharing a single vertex.
![\begin{array}[]{|l|l|l|l|l|}\hline\Gamma&a_{1}&a_{2}&a_{3}&a_{4}\\
\hline\circ-\circ-\circ-\circ&(0,0,0,1)&(0,0,\sqrt{\frac{3}{4}},\frac{1}{2})&(0,\sqrt{\frac{2}{3}},\sqrt{\frac{1}{3}},0)&(\sqrt{\frac{5}{8}},\sqrt{\frac{3}{8}},0,0)\\
\hline\circ\stackrel{4}{-}\circ-\circ-\circ&(0,0,0,1)&(0,0,-\sqrt{\frac{1}{2}},\sqrt{\frac{1}{2}})&(0,\sqrt{\frac{1}{2}},-\sqrt{\frac{1}{2}},0)&(-\sqrt{\frac{1}{2}},\sqrt{\frac{1}{2}},0,0)\\
\hline\circ-\circ\stackrel{4}{-}\circ-\circ&(0,\sqrt{\frac{1}{2}},-\sqrt{\frac{1}{2}},0)&(0,0,-\sqrt{\frac{1}{2}},\sqrt{\frac{1}{2}})&(0,0,0,1)&(\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2})\\
\hline\circ-\circ-\circ\stackrel{5}{-}\circ&(0,0,1,0)&(0,-\frac{\sqrt{-\tau+3}}{2},\frac{\tau}{2},0)&(0,-\sqrt{\frac{\tau+2}{5}},0,-\sqrt{\frac{-\tau+3}{5}})&(\frac{\sqrt{2-\tau}}{2},0,0,-\frac{\sqrt{\tau+2}}{2})\\
\hline\end{array}](mi/mi207.png) |
(15) |
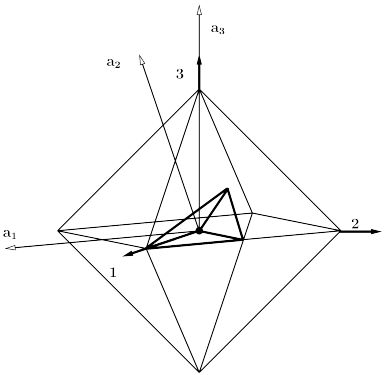
Each Platonic spherical polyhedron forms the
prototile of a regular tiling of the 3-sphere. The Platonic tilings are well-known
regular m-cells, known as
convex regular 4-polytopes.
The ![]() -cell is illustrated in Fig.21.
-cell is illustrated in Fig.21.
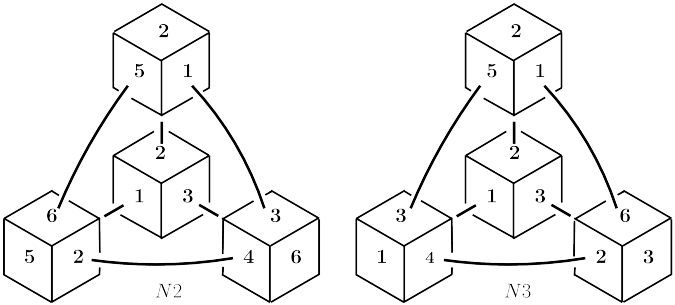
All possible homotopies of the Platonic polyhedra on the 3-sphere were derived by Everitt [11]. His algorithm gives the gluing prescriptions of polyhedral faces and edges. They describe how faces are rotated around their midpoints and then glued in pairs. A remarkable outcome of his analysis is that, for a fixed polyhedral shape of the regular polyhedron, there are distinct possible homotopies. We list them in Table 2 from [41]. An example is given in subsection 2.6.
| Coxeter diagram |
Polyhedron |
Reference | |||
| tetrahedron |
[38] | ||||
| cube |
[39] | ||||
| cube |
[39] | ||||
| octahedron |
[40] | ||||
| octahedron |
[40] | ||||
| octahedron |
[40] | ||||
| dodecahedron |
[36], [37] |
The first distinction between them is in the gluing of faces and edges [41]. For a fixed polyhedron, different homotopic boundary conditions are fulfilled.
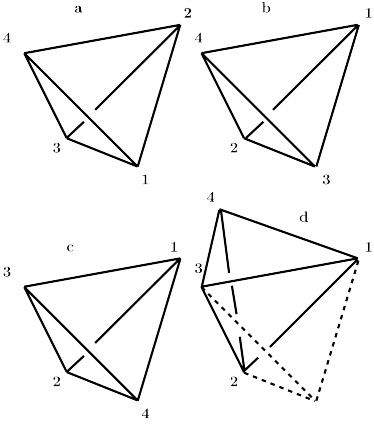
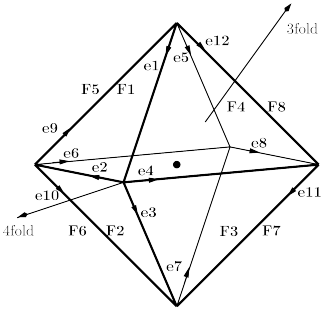
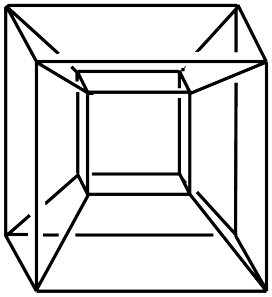
In the following figures we show the tetrahedral, cubic and octahedral 3-manifolds and their face and edge enumeration.
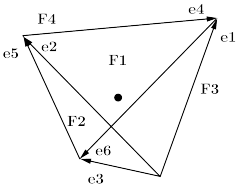
In the following Fig16 we illustrate the action of the cyclic generator of deck
transformations for the tetrahedron ![]() .
.