§ 2.3. Point symmetry.
If the manifold is a regular polyhedron, we can examine its point symmetries which preserve the center.
For the interval ![]() we can ask for its
point group
symmetry operations preserving the center
we can ask for its
point group
symmetry operations preserving the center ![]() .
The only non-trivial operation of this type is the reflection
.
The only non-trivial operation of this type is the reflection ![]() .
With respect to functions on the interval
.
With respect to functions on the interval ![]() we can ask for a basis of functions
on
we can ask for a basis of functions
on ![]() invariant under this reflection. Clearly we must replace the exponential functions
by the combinations
invariant under this reflection. Clearly we must replace the exponential functions
by the combinations ![]() , and the
expansion eq.11 must be replaced by
, and the
expansion eq.11 must be replaced by
 |
(12) | ||||
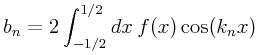 |
These basis functions have both periodicity and reflection symmetry. The restriction to reflection symmetry reduces the set of basis of the Fourier series roughly by a factor two.
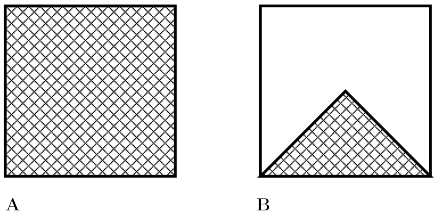
In Fig.13 we illustrate the effect of 4fold point symmetry of the square in the Euclidean plane, which is the universal covering of the torus. The domain of definition of functions is restricted from the full square A by 4fold point symmetry to the sector shown in B. It is easy to find the corresponding restriction on the basis functions eq. 13 for the functional analysis.