§ 2.2. Functional analysis and topology.

Physics describes objects by functions on appropriate domains. Functions on a manifold ${\cal M}$ must respect its topology.

Example 1c: Functional analysis on the circle. We model the circle by the interval $J=\{-1/2,1/2\}$ on the real line. Consider on $R^{1}$ all exponentiaL functions

$f_{k}(x)=\exp(ikx),\:-\infty<k<\infty.$

(9)

Their values will be unique on the domain $J$ provided they are periodic, that is

$f_{k}(x+1)=\exp(ik(x+1)):=f_{k}(x)\exp(ik)=f_{k}(x).$

(10)

Periodicity requires $k=k_{n}=n\: 2\pi,n=0,\pm 1,\pm 2,...$ , and so restricts the values of $k$ to the discrete subset $k_{n}$ . The discrete subset $f_{{k_{n}}}(x)$ of functions on the interval $J=\left[-\frac{1}{2},\frac{1}{2}\right]$ fulfills the homotopic boundary condition $f_{{k_{n}}}(1/2)=f_{{k_{n}}}(-1/2)$ .

Repetition of the discrete translation step eq.10 generates the discrete translation or infinite cyclic group $C_{{\infty}}$ . The periodic set $\exp(ik_{n}x)$ is the basis of complex Fourier series analysis of a periodic function. It represents any periodic function as an infinite series with complex coefficients $a_{n}$ . These can be found by integration over the interval $J$ :

			$\displaystyle f(x):f(x+1)=f(x),$		(11)
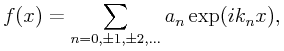			$\displaystyle f(x)=\sum _{{n=0,\pm 1,\pm 2,...}}a_{n}\exp(ik_{n}x),$
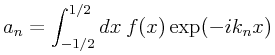			$\displaystyle a_{n}=\int _{{-1/2}}^{{1/2}}dx\: f(x)\exp(-ik_{n}x)$

We conclude that the particular functions $\exp(ik_{n}x),\: n=0,\pm 1,\pm 2,...$ form a basis of all functions on the circle $S^{1}$ and, when extended from the interval $J$ to the real line, of all periodic functions on the line.

A useful and constructive characterization of the basis of Fourier analysis arises in terms of the deck transformation group: Any basis function is invariant under the action of the discrete translation group $H={\rm deck}(S^{1})$ , which in turn is isomorphic to the fundamental group $C_{{\infty}}$ of the circle. In case of the circle it suffices already to require the invariance under the generator of the translation group, that is to require periodicity eq. 11.